Métodos Multipasos para Ecuaciones Diferenciales
¡Bienvenidos al Método Multipasos!
Método Multipasos
Los métodos de un paso como Runge-Kutta calculan cada punto de la solución de una E.D.O. a una distancia \(h\) utilizando la información del punto anterior. Los métodos de pasos múltiples son fórmulas que utilizan varios puntos calculados y disponibles para calcular la solución en un nuevo punto.
Fórmulas de pasos múltiples de predicción
Estas fórmulas se usan para calcular la solución en un punto mediante un polinomio de interpolación colocado en varios puntos anteriores conocidos espaciados a una distancia \(h\).
En el siguiente gráfico se supondrán conocidos los puntos \(y_{i-k}, \dots, y_{i-3}, y_{i-2}, y_{i-1}, y_i\) mientras que se desea calcular el punto \(y_{i+1}\).
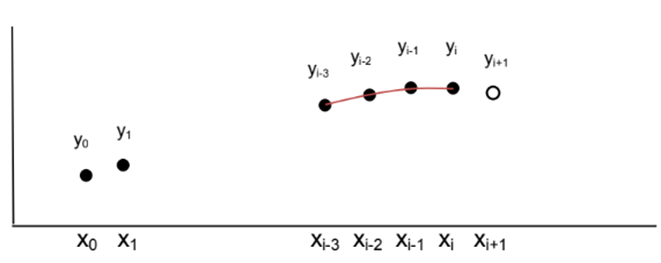
Obtención de la fórmula de pasos múltiples:
Dada la E.D.O.
\[y'(x) = \frac{dy}{dx} = f(x,y), \quad y(x_0) = y_0\]Reescribir como
\[dy = f(x,y)\,dx = y'(x)\,dx\]Integrando desde un punto conocido \(y(x_{i-k})\) hasta un nuevo punto \(y(x_{i+1})\):
Para obtener una fórmula aproximada se usa el polinomio de diferencias finitas regresivas incluyendo al punto \(i\) y los puntos anteriores.
Sustituyendo el polinomio y cambiando los límites y el diferencial:
Se obtiene la siguiente expresión con la que se pueden generar fórmulas de pasos múltiples denominadas fórmulas de predicción.
La fórmula tiene dos parámetros para elegir: \(n\), \(k\)
Observaciones importantes:
- Las fórmulas de predicción requieren tener puntos disponibles antes de su aplicación. Estos puntos deben ser calculados con mucha precisión. El método adecuado para esto es el método de Runge-Kutta.
- La integración extiende el polinomio de interpolación hasta el punto \(i+1\) que no pertenece al dominio del polinomio. Por lo tanto, se ha realizado una extrapolación, que en general no produce resultados confiables.
- La ventaja de estas fórmulas es que requieren menos cálculos en cada paso pues usan puntos ya calculados. Esto fue importante en la época en la que no se disponía de dispositivos computacionales automatizados. Una aplicación de interés es usar el método para proyectar el valor de una función y su derivada fuera del intervalo que contiene a los puntos conocidos.
Fórmulas de pasos múltiples de corrección
Estas fórmulas son el complemento a las fórmulas de predicción. En las fórmulas de pasos múltiples de corrección se coloca el polinomio de interpolación incluyendo el punto \(i+1\) calculado como una primera estimación con la fórmula de predicción. El nuevo resultado corrige el resultado anterior y produce una mejor aproximación.
Dada la ecuación diferencial ordinaria de primer orden:
\[y'(x) = \frac{dy}{dx} = f(x,y)\]Reescribirla como
\[dy = f(x,y)\,dx = y'(x)\,dx\]Integrando desde un punto arbitrario \(y(x_{i-k})\) hasta el punto desconocido \(y(x_{i+1})\):
Para obtener una fórmula aproximada de corrección se usa el polinomio de diferencias finitas regresivas incluyendo al punto \(i+1\) y puntos anteriores.
Sustituyendo \(y'(x)\) por el polinomio y cambiando los límites y el diferencial:
Esta expresión se usa para generar fórmulas de pasos múltiples de corrección.
La fórmula tiene dos parámetros para elegir: \(n\), \(k\)
Métodos de Predicción – Corrección
La combinación de una fórmula de pasos múltiples de predicción con una fórmula de pasos múltiples de corrección constituye un método de Predicción – Corrección. Uno de estos métodos que ha sido estudiado se denomina fórmula de Adams – Moulton. Se la obtiene con los parámetros \(n = 3, k = 0\) en las fórmulas establecidas anteriormente. El desarrollo detallado permite también conocer el error de truncamiento correspondiente.
Fórmula de Predicción de Adams-Moulton:
\[y_{i+1} = y_i + \frac{h}{24} \left[ 55f_i - 59f_{i-1} + 37f_{i-2} + 9f_{i-3} \right],\] \[\quad E_p = \frac{251}{720} h^5 y^{(v)}(z)\]Fórmula de Corrección de Adams-Moulton:
\[y_{i+1} = y_i + \frac{h}{24} \left[ 9f_{i+1} + 19f_i - 5f_{i-1} + f_{i-2} \right],\] \[\quad E_c = -\frac{19}{720} h^5 y^{(v)}(z)\]Esta combinación de fórmulas permite establecer un esquema de exactitud para el error de truncamiento con el planteamiento siguiente:
Sean:
- \(y_{i+1}\): valor exacto, desconocido
- \(y_{i+1,p}\): valor calculado con la fórmula de predicción de Adams-Moulton
- \(y_{i+1,c}\): valor calculado con la fórmula de corrección de Adams-Moulton
Suponer que los valores de las derivadas en el error son aproximadamente iguales.
Considerando la siguiente disposición de los valores calculados y el valor exacto:

Para aplicar este criterio, suponer que se desea que el error en el resultado final de \(y_{i+1}\) calculado con la fórmula de corrección no exceda a \(E_c < 10^{-m}\), entonces deberá cumplirse:
\[| y_{i+1,c} - y_{i+1,p} | < 14 \times 10^{-m}\]Si no se cumple, debe entenderse que el valor de \(h\) tendría que reducirse para reducir el error.